MPM1D1 - Day 75 Snow Day

The buses were cancelled today and as a result I had very few students show up. I did have one girl email me to see if she could write her test today. She came, got some help with a few things and wrote her test. Good for her.

I did have a number of struggling students request some extra work to do over the holidays. I was impressed with their desire to improve. So I sent them some work.

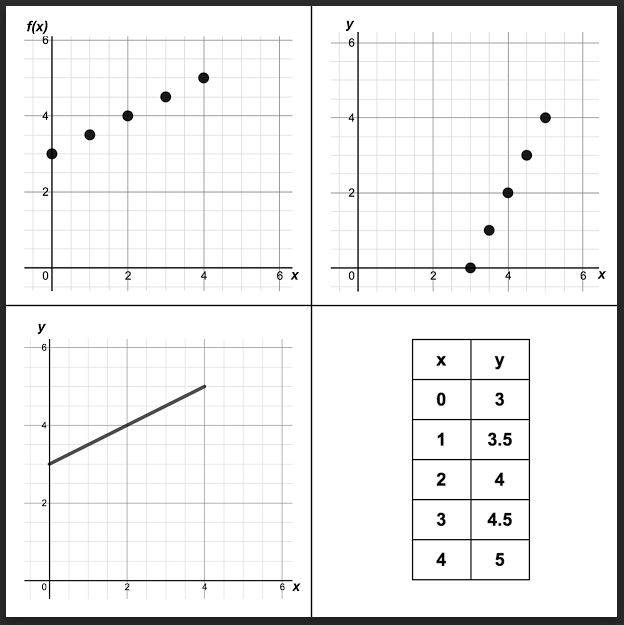
MPM1D1 - Day 74 Test Review

We started today by looking at these two objects that were printed yesterday.

The goal was to consolidate some of yesterday's work and to reinforce one of yesterday's big ideas. Because of the work my students had done with their pentominoes, they knew that each pentomino was made up of five cubes. The cubes on the small pentominoes were 0.5 cm in all direction and the cubes on the large one were 1 cm in all directions. So, I asked how many times bigger the volume of the larger one was compared to the smaller. I received a couple of answers of 2 (which I expected), an answer of 4 (with the justification that that's what they found yesterday) and an answer of 8. I held the figures up and asked if anyone thought it would only take two of the little ones to fit into the bigger one. Strictly by intuition everyone knew that 2 couldn't be the answer. One student offered up an explanation of doubling in more than one dimension. At this point we jumped into a bit of algebra and looked at an expression for the volume of a cube that was x units long and compared that expression to one for a cube that had a length of 2x.

The large figure in the picture is a model of an original that is twice the size, in all dimensions. I asked how many of the little ones would fit in the giant one.

There was some discussion about 16 vs. 64, but eventually we settled on 64 (supported with some algebra). Once the relationship for volume was squared away we quickly touched on the relationship for surface area.

It was a good, fun discussion that I think made a lot of sense because of the manipulatives on hand, that were made by the students.

After the warm-up we wrote a mastery test on equations of lines then students continued working on the review for their test tomorrow.

MPM1D1 - Day 73 Finishing Up 3D Printing

Today we picked up right where we left off yesterday with the pentomino activity. We fired up the 3D printer and started printing right away. Groups that hadn't finished the calculations from yesterday kept working away. They stumbled a little with the different units but eventually most of the groups figured things out. We printed one figure after another but eventually ran out of time. I'll get the others printed at some point.

Once groups were done I gave a review for them to work on to prepare for this week's test. I was hoping to do the test Thursday, but after things didn't go well yesterday I figured they would need an extra day. So, yes we are having a test on the last day before the holidays. It's not ideal, but I figure it's better than doing the test Thursday or after the holidays.

Generally, most students worked well today, either on the pentominoes assignment or the review. There was also a fair bit of excitement when a group's pentomino began printing.

During the printing process today I remembered that prints were not solid plastic. They are infilled with either a hexagonal pattern or a rectilinear pattern. I'll have to do some research to see what percentage we were infilling. This actually adds another layer to the assignment. The more I think about it, the more I think this activity would make a great culminating activity.

MPM1D1 - Day 72 Surface Area, Volume & 3D Printing

I had seven students away yesterday so I spent some time at the beginning of the period recapping what we did yesterday. Once the recap was done we moved right into some volume and surface area.

My own kids have a pentomino based game called Katamino. It's a fun game that really stretches your spatial reasoning skills.

I thought it would be fun to make this game the basis for an assignment. If you don't have the game you could always modify the assignment to work with any pentominoes or even have students build their own figures using linking cubes.

The gist of the lesson is that students get a pentonmino and calculate its surface area and volume. Then they create a scale diagram of a pentomino that is half the size (in all dimensions) of their original pentomino. They calculate the surface area and volume of their model and make note of the relationship between the original and the half-sized model.

They were given the length of a spool of filament (in metres), the diameter of the filament (in millimetres) and the cost of the spool and they needed to determine the cost of their pentomino. Once they had done all of that they designed their pentomino in TinkerCAD. The designing was pretty simple and didn't take long at all. Once their design was complete they were able to print on the 3D printer.

This was meant to be a bit of a fun lesson but for whatever reason many students didn't seem to be into it. I had students working in pairs which is not something we normally do. They also weren't working at the board. Some students spent a lot of time fidgeting with the pentomino (I thought fidget spinners were so last year?), others watched as their partner did the work. One group took 30 minutes just to get their measurements, despite repeated calls to get going. I think next time I need to get groups to do their work at the whiteboards and maybe I need to be explicit about how they could split up their work. Maybe groups of three would have been better than pairs. I'll have to rethink the logistics of this one.

Having said that I had two groups print today. They did a great job and were pretty excited about the result. I had one more group that finished everything except for the printing at lunch. They will print first thing tomorrow. We will finish up tomorrow. I'm looking forward to trying this again to see how it goes.

Here's a description of the task. This task could also be used in an MFM2P class. I've also modified the task to fit the MBF3C course. You can find that here. Here is a link to a quick introduction to TinkerCAD.

MPM1D1 - Day 71 Rearranging Formulas

We started today practicing solving equations with fractions as groups at the whiteboards. Here we the warm-up questions.

There weren't any problems with the first question. There were a couple of problems with the second one and more problems with the third. We spent some time working through the issues. Some groups wanted more questions to practice with so I had them make up their own and go from there.

Once everyone seemed comfortable solving these equations we moved on to rearranging formulas. I posted a few on the board and let them get to work. Here are the questions they started with.

The most challenging one here seemed to be part c. For groups that struggled I gave them an example where y, m and b were given and asked them to solve for x. They had no trouble doing so, so I asked them to replace the numbers with variables. That seemed to be enough to get them going.

Once groups were done I gave them some questions to practice.

MPM1D1 - Day 70 Equations of Parallel and Perpendicular Lines

During yesterday's warm-up, one group was convinced that two of the lines were perpendicular. Based on that comment I thought today's warm-up should be about perpendicular lines.

Once groups found equations for the lines I asked what they knew about how the lines intersected. They responded with the point of intersection and I asked if there was anything else. When they told me that the lines were perpendicular I asked how they knew the lines were perpendicular. Some groups could justify their claim immediately, while others need time to formulate their ideas.  

After the warm-up we moved right into finding equations of parallel and perpendicular lines. We had a conversation to remind them about how to find the equation of a line given two points and what it means for lines to be parallel or perpendicular. They worked on these problems at the board:

None of the groups had any trouble with the first two questions. A couple of groups struggled with the third and all groups needed some reminders about rearranging equations for the last question. When they were finished they went to work on some practice questions.

MPM1D1 - Day 69 Properties of Quadrilaterals

The warm-up for today was to find the equation of the line segments shown below.

I figured this would be a good opportunity to practice dealing with horizontal lines, as well as others. One group tried using the formula for slope but when I asked if there was an easier way they told me that they could use the graph. Another group was convinced that the two segments on the right were perpendicular. When I asked if they could explain how they knew this was true, they began doubting themselves and then verified that they were in fact wrong by looking at the slopes of each.

The goal for today was to investigate properties of quadrilaterals. I found this Geogebra activity. I had originally thought that I would make something up but finding this saved me some time.. Students worked through the activity at their own pace and took notes about what they observed. Some notes were better than others. I had students working individually on their own computers. I'm thinking it may have been better to have them working in pairs.

Once most students were done I summarized with this graphic:

Then it was time for some practice. I gave these questions from this page. Some students chose to work in groups at the board, some chose to work in groups at their desks and some chose to work individually. The two strongest students, who hated working with each other earlier in the semester, decided to team up along with a third person because they realized they could get the work done faster if they worked together. They stayed in past the bell and got it done.

MPM1D1 - Day 68 Speedy Lines

We started with a visual pattern today:

It was interesting to see how students counted the number of watermelons in each step. It seemed as though most groups had a couple of different ways of counting which made for some interesting discussions. I think the hardest part here was generating the table of values. Once they had that, groups quickly came up with the equation and the number of watermelons in the forty-third step.

We took up the equations mastery test from yesterday and hopefully cleared up some misconceptions.

Today's main event was practicing coming up with the equation for a line of best fit. Everyone can draw a line of best fit but when I ask for the equation many students go to their tables to find the slope. When they do this they don't always choose points that are on the line. We need to work on realizing that we want to use points that are on the line to find the equation.

Today we timed to see how long it takes to assemble 5,6,7,8,9 and 10 linking cubes. This is an idea that I modified from Mary Bourassa's Speedy Squares. Rather than making squares we just connected cubes to form a line. Groups worked to collect data. Some groups needed to work on being consistent but got it sorted out pretty quickly. Then they plotted the data and worked to find an equation of the line of best fit. They then practiced using their equation. Here's the handout.

With about fifteen minutes to go we tried the mastery test on solving equations again.

It occurred to me at the end of the period that I don't take enough pictures of students working or of their work. Something to work on. Sorry about the lack of photos.

MPM1D1 - Day 67 Solving Systems of Equations

When I first came across today's warm-up question I thought it would be great as a measurement problem solving type question with a bit of algebra thrown in for practice. Here is the problem:

What I did not anticipate was that this was also a great problem for solving systems of equations. A number of groups realized quickly that they needed an expression for the perimeter of each rectangle and then they had to set them equal to each other. One group quickly said "We don't know how to find the length". I asked them to start with what they did know and go from there. This quickly got the group moving forward.

I was amazed to see how easy most groups were able to set the equations equal to each other and solve. For whatever reason they were far better at this than they were last week. I'm guessing it has something to do with the context here. They can see the perimeter and know that the perimeters have to be the same (since it says so in the question). I was very impressed with the results today. One group that finished early said something along the line of "You're going to ask us to find the area next, aren't you?". Too be honest I hadn't thought about that, but it seemed like a great extension for those who were done. So I asked them to find an expression for the areas and asked if they could expand their expressions. What a great way to lead them into multiplying binomials. I love using the great ideas that students have.

The goal for today was to have students solve systems of equations graphically (the course only gets as far as solving by graphing). I mentioned earlier, we did this about a week ago. The nice thing about spiralling is that you can visit some trouble areas. This was one of those areas and I wanted to extend a bit by looking at systems in different forms.

Here are the questions I had them work on:

There were so many great questions that came out of this work. I find students always have a hard time with the equations of vertical and horizontal lines so a bit of extra practice here is alway good. Some students struggled with graphing the second equation in part b). They forgot what the slope was if there was no coefficient showing in front of the x. There was lots of good practice graphing equations and finding ways to graph different forms of equations.

One girl in the class insisted on solving the equations by substitution. This is easy enough for the first five questions, but I'me guessing she'll have a hard time with the last couple.

With about 15 minutes to go we moved onto a mastery test on solving equations.

MPM1D1 - Day 66 More Equations With Fractions

We started with the following Fraction Talks, where students had to determine which fraction of the picture was red.

It was interesting to hear all the different ways students did these. Their were some good discussions about adding and multiplying fractions, which was a good reminder for some.

I then put the following equations with fractions on the board and had students work individually to solve them.

A couple of people asked for a refresher on how to solve equations with fractions so we worked through a question as a class, then they began working away. It was slow going for some, but everyone was moving along and getting a little better. Lots of students were those in their groups who were struggling.

Once they were done, students continued the handout from Friday. It was a good day of individual work.

MPM1D1 - Day 65 Solving Equations With Fractions

We started with this Which One Doesn't Belong:

It was great to hear all of the terminology that came out of the discussions.

After the warm-up we moved into solving equations with fractions up at the board in groups. I didn't give any instructions. I gave some equations for groups to solve and they did a great job.

Here are the questions they worked on:

I was amazed at how well the groups worked. They required little to no assistance from me. They were able to apply what they had learned about solving equations without fractions and things worked out great. It was also great to see the stronger students really working with those that struggled to bring them along. I feel that we've really developed a community of learners in the class and I'm really happy about that. One of the groups consisted of two students who pretty much refused to work with each other at the beginning of the semester. Today they worked as though they were good buddies.

Once the groups were done I brought the class together and asked what was different about the equations today. Many students said that these equations were more difficult. When I asked why they were more difficult the response was because of the fractions. We then talked about how we could eliminate the fractions by multiplying both sides of the equation by a common denominator. We did a couple so they could see how it was done then they did the first part of this handout.

MPM1D1 - Day 64 Test Day

We had our test today. Students worked away diligently and asked for clarification as needed. I'm hoping for some good results. There are a few topics that we'll revisit in the coming weeks to solidify understanding.

MPM1D1 - Day 63 Another Day of Review

The plan for today was to have students write their individual tests. But, based on what I saw yesterday during the group test, many students would not have been prepared to write today. I decided to give the class another day to work on the review questions.

At the beginning of class I made the rounds and discovered that very few students had done much of the review at all. I was a little disappointed.

Most students used their time wisely today. It was great to see some of the stronger students helping those that were struggling.

Here's hoping for good results tomorrow.

MPM1D1 - Day 62 Group Test

Today was our group test. I let students choose their own groups. I'm not sure whether this was a good idea or not. It seemed that some students weren't really sure who to work with. Others had a good sense but I had said that the group must be three people. This meant that those hoping to be a group of four had to decide who was going to leave. Not doing random groups today made me really appreciate doing random groups.

Each group received the test and started working on their whiteboards. I had each group start at a different question. Some groups were very efficient and others really seemed to have a hard time making headway. I went around and did lots of listening and asked if students could clarify their thinking for me.

It was pretty obvious that many students had not studied for the test. There were lots of incorrect assumptions being made along with lots of simple errors. I really like the group test because of all the discussion and learning that is taking place. I also like the fact that I have some conversations (which I recorded today) that I can use to supplement (one way or the other) a student's test results. What I don't like about this extra information is that I don't have a clean way to count it.

I struggle with how to assess the group test (and maybe it just needs to be formative). I don't want to penalize a student who learned a ton between the group test and the individual test. I also don't want students to feel like they did well on the group test so they don't need to prepare for the individual test. In any case, I do have a record of the conversations along with photos of all the work that I can use to help in making an overall judgement.

The plan for tomorrow was to do the individual test but I don't think my students are ready for that yet.

MPM1D1 - Day 61 Solving a System of Equations Algebraically

We started the class solving some equations. I wanted students to really focus on showing their work and being methodical in their approach.

After the warm-up we looked at solving a system of equations algebraically. We looked at the Knotted Rope work we did last week and discussed the ways we could determine when the ropes would be the same length. Students mentioned that they could graph it or look at the table. I asked how many of them wanted to fill in the table to get up to 60 knots. We decided that in this case a table would take too long and one student suggested we should use an equation. We talked about how if the lengths of the ropes were equal then the equations representing their lengths must also be equal. I helped them setup the equation and let them solve it.

For the remainder of the period students could work on their own or in groups on the review for the upcoming test.

MPM1D1 - Day 60 More Knotted Ropes

We started with another Which One Doesn't Belong.

The goal here was to connect the different representations of a linear relation. Students did a great job of discussing slope, y-intercepts, x-intercepts, continuous, discrete and the equations for these relations.

They then had some time to finish up the Knotted Ropes work that they started yesterday.  The groups were much more focused today. They graphed the relationship between rope length and number of knots for each roe. They generated an equation and made connections between the slope and y-intercept and what they meant in terms of the rope. I asked them to use there equations to find how long will each rope be if it had 25 knots? How many knots are needed to get each rope to a length of 60 cm? Then they plotted their data in Desmos and performed a linear regression to get the equation of the lines best fit. They then checked on the graph to see where the point of intersection was located.

I had hoped to look at how to find the point of intersection algebraically but one or two of the groups weren't quite ready for it yet. I'll pick up here on Monday.

Some groups finished early so I gave them some more parallel and perpendicular lines practice. We're having a test next week so I also gave out the test review in case anyone wanted to get started on it over the weekend.

MPM1D1 - Day 59 Knotted Ropes

The warm-up for today was this Which One Doesn't Belong:



It was a nice tie in to what we have been doing (slopes, intercepts, parallel lines) and I heard some great reasons for each one not belonging.

After the warm-up we consolidated the work that we did yesterday on parallel and perpendicular lines. 

The goal for today was to have students explore the relationship between the number of knots in a rope and its length (inspired by this post). Each groups received a length of rope and a length of string. 

They were to create a table, graph and equation to represent both their rope and string, then determine how many knots were needed to make both ropes the same length (same number of knots in each rope). We only had about 30 minutes to complete the activity. I knew that students wouldn't finish but was hopeful. Most groups worked very effectively, but a couple couldn't seem to measure accurately enough. I might need some larger diameter rope that doesn't stretch so much. A number of groups found that their rope was longer after adding a knot to it.

Nobody got past the graphing stage so we'll finish up tomorrow.



MPM1D1 - Day 58 Parallel and Perpendicular Lines

Today's problem was one that I was reminded of at a recent professional development session (thanks @chrisleechss ).

This question generated a lot of discussion. Is 1 a big slope? Does it matter if it's negative or positive?  There were lots of good conversations as students continued to solidify their understanding of slopes. For groups that finished early I asked how their answers would differ if they were allowed to use the numbers 0-9.

The consolidation of this problem led us to talk about horizontal and vertical lines. We talked (again) about the slopes of these lines but we also talked (unexpectedly) about the equations of horizontal and vertical lines.

The main lesson for today was investigating parallel and perpendicular lines. I gave this investigation. It was good for students to practice graphing lines but I think I need to rework it for them to get more out of the perpendicular lines portion.

We'll consolidate the investigation tomorrow.

MPM1D1 - Day 57 X- and Y-Intercepts

It's been a while since we did any work with percentages so today we looked at this Would You Rather problem:

Some groups were quick to choose a price and start working with it. Other found 40% of 15 and 50% of 25 and chose the smaller number :(. I asked what those numbers meant and eventually got them headed in the right direction. When the first group finished I asked if the price of the book made any difference? Was there better deal always a better deal regardless of book price.

Once groups finished I asked them to do the following:

I talked individually with groups about what they knew about the y-intercept. We arrived at the fact that they x-coordinate was always 0 and off they went. Having never done this before some groups struggled a bit. I brought the class together for a couple of minutes and we talked about what it means to be an x- or y-intercept. They went off and completed the questions above in their groups. When they were done they worked on question 2 from yesterday's handout. After everyone was done the questions above we consolidated and wrote a quick note. Students then finished up the practice questions.

MPM1D1 - Day 56 Another Kick at Success Criteria & Standard Form

Last week students looked at an incorrect (level 2) solution to the problem below.

They did a good job with it, but I wanted to take some time today to model how to solve a problem and to develop some success criteria for problem solving.

I gathered students at a whiteboard at the back of the room and we started working on the problem. As we worked through the problem I would periodically stop and ask what we had just done. The peer tutor wrote a list on a different board of all the things we talked about. Here are some of the things we talked about:

Once we were done most students really wanted to get a picture of the list. I guess something about our process spoke to them as being important. We'll come back to the criteria next time I give out a problem.

The plan for today was to look at the equation of a line in standard form. I had groups do the following:

Some of them struggled a fair bit with part b, but other groups blasted through it quickly. Once they were finished we talked briefly about what standard form is and consolidated how to convert from standard form to slope/y-intercept form (since many groups ended up doing some rearranging when making a table of values).

We did an example, then I gave out some practice questions (question 1).

MPM1D1 - Day 55 Error Finding and Angle Theorems

Today's warm-up was a little different. We started by looking at a problem with a fully worked solution. The solution contained errors (it was a level 2 exemplar) and students had to identify the errors then present a complete (level 4) solution.

I gave out a page with two problems along with the level 2 solutions.

The first problem served the purpose of practicing some of the algebra skills that we worked on earlier in the week, that need more work.

I had students work in groups of three up at the board to figure out what happened in the solution. This was difficult for some students. They just wanted to solve the problem their way, which was different from the solution. Once groups figured out the approach used in the problem they were able to determine where the errors were and correct them. There were some good discussions about how to fix those errors. I think students were able to solidify their understanding of the distributive property and collecting like terms.

As a result of this activity my class has now constructed an exemplar for solving these open response type questions. I'm hopeful that next time we solve a problem like this, we will be able to co-construct the success criteria for solving problems like this.

All groups completed the first problem, many were working on the second problem and one group finished both.

We then moved onto this activity (thanks @davidpetro314) to investigate parallel lines, transversals and angle theorems. This was review for most students and most of them seemed to remember doing it in grade 8. Once they were finished with the activity I had them create their own note for their notebooks to remind them of the theorems. Some of the notes were excellent, others were not, but who am I to say what type of note would be useful for all students. I then gave them some questions to practice.

MPM1D1 - Day 54 Finishing Up Barbie Bungee

Today we finished up Barbie Bungee. A couple of groups wanted to collect more data or double check some of their data from yesterday. Students began analyzing the data. They were creating graphs, both by hand on using Desmos. They were extrapolating using their graphs. They were coming up with the equation of their line of best fit. They were performing linear regressions in Desmos and comparing it to their findings. There was a lot more reasoning about the reasonableness of their answers than I expected. Once students had a number of rubber bands they were happy with they began writing their reports.

With about twenty minutes left we headed to the stairwell to see who could get Barbie the closest to the floor without hitting it. It was so much fun. We had one person at the bottom recording in slow motion. Some students were at the top of the stair watching, while others chose to observe from below. The closest group had Barbie touch the floor with her outstretched hand, but not touch her head. There was some debate about this should count or not. What do you think?

I haven't received a copy of the video yet but once I do I will post it.

What a great end to a great activity. I can't wait to read the write-ups.

MPM1D1 - Day 53 Barbie Bungee

We skipped the traditional warm-up today and got right into Barbie Bungee. Our warm-up was co-constructing the success criteria.

As students came into class they received a card (as they always do) that would assign them to a random group. After the bell went I had students gather at a white board at the back of the room. I explained that each group would receive a Barbie and they had to figure out how many rubber bands to tie onto Barbie so that she got as close to the floor without hitting it when she was dropped from the stairwell. I told them that this was an assignment and I wanted them to go to their boards and come up with a list of criteria that they thought should be included in their assignment. I felt like after the time we spent working on the success criteria  for the Pumpkin Time-Bomb assignment, students had a good sense of what should be included in an assignment.

I was not disappointed. The results were far better than they were the first time we co-created success criteria. Each group created a good sized list of useful criteria this time around. After about 10 minutes I stopped them and had them group their criteria into categories of their choosing. As it turned out most, if not all groups, created three different categories. The categories were roughly Data (needed/given/measured), Mathematics (graph, table, equation, line of best fit), Report (description of task and process used, showing your work, proper terminology, units etc.).

I brought the class together, we talked about the categories and some of the items in their categories. I told them that I would organize all of their ideas and send them a written copy via email.

I handed out the Barbies and seven rubber bands and let them go. There were lots of ideas floating around that led to some great thinking.

• We could measure one band and multiply by seven. 
• Should we measure them stretched or not?
• Let's measure from the floor up.
• Our measurements weren't very accurate (In one case adding a 10cm band only added 2cm to the distance Barbie fell).
• Let's do three trials at each level and take an average.
• We should each trial, then watch the video to see how far Barbie fell.

The data collection was time consuming and messy at times but in the end every group came away with a set of data they felt comfortable with. Although it was time consuming I think having students struggle through those difficulties and errors was very worthwhile.

Tomorrow they'll start to analyse their data and begin putting together their individual reports, which will be due sometime next week.

MPM1D1 - Day 52 More Optimization

We started with a quick Estimation 180 to order the glasses from smallest capacity to largest.

Then picked up right where we left off on Friday. Friday some groups did a cylinder question and some did not. It was great to have students working in different groups today. It allowed the expertise to flow through the room. They worked on the two problems below.

The groups that didn't have anyone who had seen a similar problem naturally struggled. I spent some time working with them, but I think they would benefit from some more practice. Once students were done they had some time to work on a couple of questions from each of the pages found on this document. Sadly, much of the individual work was seemed very unfocused. I'm thinking we'll have to revisit this topic at some point.

With about twenty minutes to go in the period I stopped them and we took up the algebra (collecting like terms and distributive property) mastery test that they wrote last week. After taking it up we wrote it again.

MPM1D1 - Day 51 Optimizing Volume and Surface Area

We started with these problems:

I gave the problems orally, one at a time and groups made their way through them. It was great to watch them work. For groups that made mistakes, it was often enough for me to say "Are you sure?" for them to think a bit about what they did and find their mistakes.

We then moved onto today's work.

This problem was closely related to yesterday's Dandy Candies only this time the side lengths didn't need to be integer values. Most groups easily made the connection to yesterday's work and quickly came up with a solution. One of the groups was really struggling so I spent some time walking them through it. 

Then we moved onto these problems:

Theses problems seemed to be at just the right level. Students seemed to be in flow for the entire period. When groups would get stuck I'd ask a question or provided a hint and off they'd go. 

The last problem I gave dealt with a cylinder rather than a rectangular prism.

A couple of groups didn't get this far today, but those that did made some great headway. A couple of groups struggled with what the cylindrical equivalent to a cube would be. I asked how they would approach the problem if the top and bottom were rectangles rather than squares. That was enough to get them going. One of the groups, on their own, actually drew a cylinder inside a cube. It was a thing of beauty. I wish I'd taken a picture of it.

We were out of time so I gave a couple of rectangular prism questions to practice for homework. We'll pick up with the cylinders again on Monday and consolidate all of the optimization.

The period flew by today. Students were right into the work. It was challenging but not so much so that they couldn't overcome the challenges. What a great period.

MPM1D1 - Day 50 Dandy Candies

We started by revisiting this type of problem:

I was curious to see how much of this work that we did a while ago they would remember. Some groups had it figured out right away. Others tried making a table which was great to see. They started with a pen that was 25 by 50 then increased (and decreased) the dimensions by 10. Which meant that they missed the optimal solution. We talked about the properties of the rectangle that seemed to give the largest area and what they noticed about it compared to the others. They quickly realized that their rectangle needed to be a square.

Before we moved onto the main event for the day we consolidated the work that we did on the distributive property yesterday. I also gave a couple of questions for them to try.

The main event for the day was Dandy Candies. I asked what they noticed and what they wondered. There were lots of good observations and a few good questions. The most common thing they wondered about was what question I was going to ask them.

We had some good discussion about volume and surface area and they had some practice calculating surface areas. Some went immediately for the formula at which point we had a discussion about what surface area actually means. No formulas were needed after that.

We finished up the class with a mastery test on collecting like terms, multiplying and dividing monomials and the distributive property.

MPM1D1 - Day 49 Area Models, Exemplars & Success Criteria

We started the class with a number talk. I asked students what 5 times 18 was. They thought quietly about it for a bit and when everyone had an answer we started sharing strategies. I told students that if they found an answer early they should try to come up with another way. I love that my students feel so comfortable with this. They work quietly and for the most part are willing to share their strategies. I also love how there are a huge number of ways to get the answer. On a previous number talk I mentioned the 'doubling and halving' strategy. It was neat to see some students using that strategy today. At the end of the talk I even had a student say "You could also double 18, halve 5 and multiply those together", which led so a good discussion about multiplying by half. Lots of great conversations.

After the number talk we revisited the distributive property, but this time using an area model. I pulled out the algebra tiles, we looked at an example as a group and then I let them try a few examples. Reactions were mixed. I heard "This is really easy" but also "I hate using these. Do we have to use them?". I think having multiple tools (the area model being one) to use can be very helpful.

Once we had practiced with the tiles we revisited our last assignment (Pumpkin Time-Bomb). The results of the assignment were not very good. My favourite was an email with one phrase in the subject and nothing else, followed by another email with another phrase in the subject and one final email with a link to a graph in the subject line. This was one student's assignment. I don't recall multiple emails using only the subject line being a success criterion.

I figured I had two options for this assignment: leave it and move on or spend some time getting it right. I opted for the latter and that's what we did today. I provided an exemplar to groups and asked them to identify the parts or characteristics that make it a good assignment. They came up with some ideas and I helped them notice a few others. They now have a good model. My only fear with providing this is that I'm going to get a class set of assignments that look essentially like the one I did. I'm willing to take a chance on this to see what happens. We will have more assignments later so I'm not too worried about a single assignment. They spent the rest of the period reworking their assignments.

I'm struggling a bit with wrapping my head around success criteria. I've had some great conversations both online and in-person with a ton of people who have more experience with this than I do. These conversations are helping me sort our some of the details but I think I'm just going to have to try a bunch of things, fail at some and repeat.

Some of the questions I had were:

• What happens when the success criteria is all 'fluff' (neatly written, includes units) and no math?
• Do I give the exemplar before we develop the criteria or after? If I give it before then am I just paying lip service to their contributions (since they have the standard in front of them)?

Some of the responses I have received are:

• Provide students with exemplars at different levels and have them assessed by students. -Melanie
• Try giving a Level 2 exemplar and asking what needs to be fixed. -@chrisleechss
• Model the creation of the exemplar with students. -@klaunderville

That last one is a big one! I think I'd like to try it but I'm worried that in doing so I will suck the thinking out of the task. I suppose I could model for a similar task and then give them the actual assignment, which would have the same or similar success criteria. However I decide to do it I'll think I'll capture some video and try to get some feedback from the video.

Thanks to all those helping me along this journey. If you have any other suggestions or comments please feel free to add them below.

MPM1D1 - Day 48 Distributive Property

We started with this Would You Rather question since we haven't done any proportional reasoning for a while.

It was interesting (yet frustrating) to watch how groups tackled this one. Some groups decided to figure out how many cups were in each package and use 'cups' as their unit rate. Some groups seemed obsessed with changing all the units to grams. Some groups wrote out some fractions but weren't really sure what they meant or what to do with them. Finally, a couple of groups figured out what they needed to do. It all took much longer than I expected it to. I sense more proportional reasoning in our future.

Things seemed to flow smoothly yesterday so we continued right along with the distributive property. Once again students worked in groups of three at the whiteboards. I gave out these problems one at a time. Some groups motored through the questions, while other groups seemed to be a little more dysfunctional. I think I need to do more get to know you type stuff every day. We did some at the start of the semester but I just kind of assumed everyone would be working well with everyone else by this point. I really like Laura Wheeler's idea of  having students introduce themselves every day and answering one icebreaker type question. It's probably a tough thing to be changing at this point but I'll keep it in mind for next time.

Once groups were finished we consolidated and I gave them some questions to practice individually.

The best part of the past couple of days was seeing students' confidence grow as they figured things out. That's what makes all of this so worthwhile.